CérénIT

Suite et fin de ma réponse au code contest après la première partie. Dans ce billet, nous allons voir comment calculer les émissions de CO2 pour la partie de trajet sur la route 66.

// Define points from the car journey on the US66 road
[
  // Here is the gts of the car datalogger
  @senx/dataset/route66_vehicle_gts

  // Here is the route 66 geoshape (+/- 20meters)
  @senx/dataset/route66_geoshape
  mapper.geo.within 0 0 0
] MAP
"onTheRoad" STORE

$onTheRoad
{
 'timesplit' 60 s
}
MOTIONSPLIT
0 GET
'sectionOnTheRoad' STORE

// Compute speed - result in m/s
[ $sectionOnTheRoad mapper.hspeed 1 0 0 ] MAP
// Convert in km/h so x3600 /1000 = 3.6 - mapper.mul expects a constant
[ SWAP 3.6 mapper.mul 0 0 0 ] MAP
'speedFrames' STORE

// Get distance between each points in km (first in meters, then in km)
[ $sectionOnTheRoad mapper.hdist 0 1 0 ] MAP
[ SWAP 0.001 mapper.mul 0 0 0 ] MAP
'distFrames' STORE

// fuel consumption approximation is  (8 liters/100km) × (speed (km/h) / 80) +1
// So it's Speed * 8 / 80 / 100 + 1 = V/10 + 1
// F = False => does not return the index
$speedFrames
<%
  0.1 *
  1.0 +
%> F LMAP
'hundredKmFuelConsumption' STORE

[ ] 'instantConsumption' STORE

<%
  'i' STORE // store index

  // Get each list and compute one by another
  // So we compute consumption for 100 km at given speed (computed previously)
  // with related distance
  // then we divide by 100 as first value is for 100 km
  $distFrames $i GET
  $hundredKmFuelConsumption $i GET
  *
  100 /
  'r' STORE
  $instantConsumption $r +!
%>
'C' STORE
0 7 $C FOR
CLEAR

// For each GTS, compute fuel consumption as 1 point
[
  $instantConsumption
  mapper.sum
  MAXLONG
  MAXLONG
  1
] MAP
// Sum all points to get total consumption
0 SWAP <% VALUES 0 GET + %> FOREACH
// 1L = 2392g CO2
2392 *
// Enjoy !

Le premier et le second bloc sont les mêmes que dans la premièr partie. Je vous y renvoie donc si besoin.

A ce stade, nous avons une liste de 8 séries correspondant à chaque section passée sur la route 66. Chaque série comporte un liste de timestamps et de points géospatiaux (lattitude, longitude, élévation).

Concernant le troisième bloc :

• il s’agit de calculer la vitesse en m/s entre chaque point de la série (ce qui explique le 1 0 0 pour prendre le point précédent, aucun point suivant et appliquer cette opération sur l’ensemble de la liste - voir la tips 3 de 12 tips to apply sliding window algorithms like an expert). Pour cela, on utilise mapper.hspeed (doc) qui consomme une série et calcule la vitesse en m/s en tenant compte de la longitude/lattitude/élévation.
• Ce résultat, on le convertit en km/h dans la foulée en utilisant mapper.mul (doc) en notant au passage qu’il lui faut une constante (on ne peut pas mettre 3600 * 1000 / mais 3.6)
• On a donc une liste de 8 séries temporelles avec chacune un timestamp, les données géospatiales et une vitesse entre chaque point. C’est stocké dans la variable speedFrames.

Concernant le 4ème bloc :

• Sur le même modèle que pour la vitesse, on calcul la distance entre chaque point des 8 séries via mapper.hdist que l’on a vu dans le premier billet. Cette fois-ci, plutôt que de calculer la distance totale, on la distance entre le point et le point suivant et on le fait pout tout les points de la liste, d’où le 0 1 0
• La distance étant en mètres, on la divisie par 1000 pour avoir des kilomètres. Mais comme il n’y a pas de mapper de division, alors on utilise mapper.mulet la valeur 0.001
• On a donc une liste de 8 séries temporelles avec chacune un timestamp, les données géospatiales et une distance entre chaque point. C’est stocké dans la variable distanceFrames.

Concernant le 5ème bloc :

• j’ai voulu calculer la consommation d’essence sur la base de la formule:

(8 liters/100km) × (speed (km/h) / 80) +1

• Cela se simplifie en Speed/10 + 1.
• Si on multiplie ce coefficient par les vitesses entre deux points obtenues précédemment (dans speedFrames), on obtient une consommation pour 100km avec chaque vitesse. Il faudra dans un second temps le pondérer par la distance parcourue entre deux points (distanceFrames) pour avoir un instantané de consommation pour la vitesse et la distance parcourue.
• Pour faire cette consommation au 100km non pondérée, on utilise LMAP (doc)pour appliquer une MACRO à chaque élément de la liste. Cette macro contient le coefficient de consommation d’essence. LMAP retourne normalement l’index et la valeur associée. Or l’index ne nous sert à rien, on met donc l’argument concernant l’index à False (abrégé F) pour qu’il ne soit pas retourné.
• On stocke le résultat dans hundredKmFuelConsumption et on a donc une liste de 8 series avec la consommation pour 100km à la vitesse donnée. Il nous faut maintenant pondérée cette liste par la distance pour avoir un instantané de consommation.

Concernant le 6ème bloc :

• On commence par créer une liste vide appelée instantConsumption.
• On sait que l’on a une liste de 8 éléments, donc on peut faire un boucle FOR (doc) dessus avec un indice allant de 0 à 7. FOR prend comme dernier argument une MACRO que j’ai nommé C
• Dans la MACRO définie au dessus, je commence par stocker l’index de la boucle. Mes deux listes de 8 séries temporelles sont identiques en terme de points, avec l’une contenant les consommations pour 100km hundredKmFuelConsumptionet la seconde les distances entre chaque point distFrames. L’idée est donc de multiplier chaque série de hundredKmFuelConsumption par la série équivalente dans distFrames et de diviser par 100 pour finir notre proportionnalité.
• On stocke cet consommation instantanée dans la variable r.
• On ajoute ce résultat r dans la liste instantConsumption, ce qui permet de reconstituer notre liste de 8 séries mais ayant pour valeur cette fois ci les instantanés de consommation entre chaque point de chaque série.

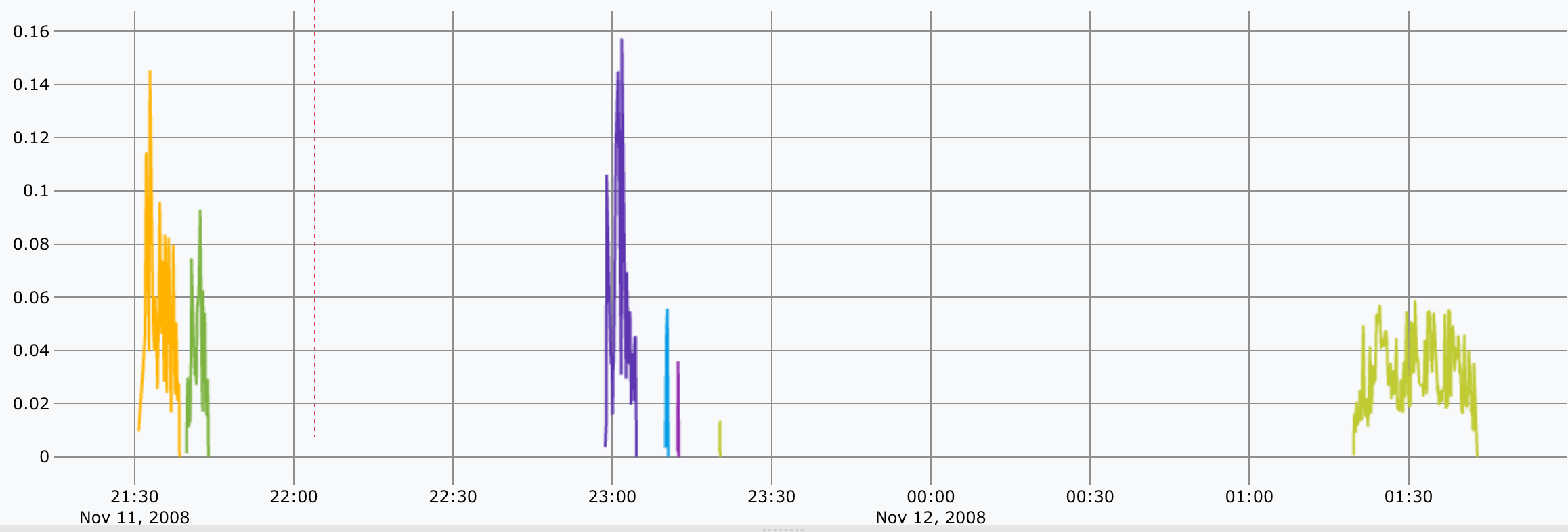
Un petit interlude visuel avant le dernier bloc :

Concernant le 7ème bloc :

• Le but est de faire la somme de chaque instantanné de consommation pour avoir la consommation totale.
• Comme dans la première partie, on utilise cette fois-ci mapper.sum (doc) en prenant l’ensemble des données des listes capturées via MAXLONG et on récupère 1 seule valeur qui s’avère être le total. On a donc la consommation totale de chaque série
• Comme vu aussi en fin de première partie, on fait alors la somme de chaque liste pour avoir la consommation totale (9.823366576601234)
• On sait que 1L = 2392g CO2, il nous reste donc à faire cette multiplication.
• On obtient alors : 23497.492851230152 ou 23,497 kg de CO2.

J’espère avoir été clair dans ces explications - si ce n’est pas le cas - dites le moi (via Twitter, Mail, LinkedIn, etc) et je préciserai les choses.

Bilan personnel de ce code contest :

• Opportunité de découvrir une partie des fonctionnalités géospatiales de Warp 10 que je n’avais pas encore utilisé
• Améliorer mon usage autour de MAP, les mapper, les MACRO et LMAP et plein de petites choses ici ou là.
• MAP s’applique sur des GTS mais aussi des listes de GTS sans rien avoir à faire. Pas besoin de se rajouter des boucles supplémentaires !
• MAXLONG utilisé dans les MAP permet de ne pas avoir à se soucier de la taille de l’élément sur laquelle on applique MAP. Cela ne fait pas non plus une erreur du style index out of range.
• en bonus, obtenir quelques lots sympathiques 😎

J’espère néanmoins apprendre des choses du corrigé officiel : Working with GEOSHAPEs: code contest results.